Algorithms: Insertion Sort

I will be writing a series of blog posts about various algorithms. The purpose of these posts will be to help me further my understanding and ability to explain algorithms. Each post will cover an algorithm, provide an implementation in a programming language, explain the algorithm using the implementation, and finally discuss any possible other discoveries I find when researching the algorithm.

What are Algorithms?

Algorithms are a fundamental part of Computer Science, but what exactly are algorithms? Well according to Merriam-Webster, they define it as:

a set of steps that are followed in order to solve a mathematical problem or to complete a computer process

In Introduction to Algorithms, algorithms are described as "a tool for solving a well-specified computational problem" and as a technology. Knuth further describes algorithms as having five important features in his book The Art of Computer Programming. These include:

1. Finiteness: it must eventually stop (better if it stops in a reasonable amount of time)
2. Definiteness: each step must be clearly stated
3. Input: Zero or more inputs to give to an algorithm
4. Output: One or more outputs the algorithm produces
5. Effectiveness: operations must be basic and producible

So why are algorithms important to study? Well just as Introduction to Algorithms describes them as tools, they should be an important tool in any programmer's tool set to allow them to go above and beyond to solve problems.

Insertion Sort

Sorting algorithms are typically one of the first algorithms introduced to students studying Computer Science. The problems are usually easy to understand; I have a sequence of objects and I want to arrange them in some ordered sequence. Numbers are often used as the objects in examples of these algorithms because ordering numbers in an increasing or decreasing sequence is simple to understand. Insertion sort is one of those sorting algorithms.

The basic high level idea of the insertion sort algorithm is given an unsorted list, each item of the list is taken out and then inserted into a list in sorted order. Well according to the definition of an algorithm, maybe what I just described is more like the strategy to come up with an algorithm. This basic strategy can thus produce multiple algorithms with different properties. I will cover two variations of insertion sort and discuss their pros and cons.

Insertion Sort on Arrays

Insertion-Sort(v)
    for i <- 1 to length(v) - 1
        j <- i
        while j > 0 and v[j-1] > v[j]
            swap v[j] and v[j-1]
            j <- j - 1

The above is the pseudocode for insertion sort taken from Wikipedia. Please note the <- operator is the assignment operator, more commonly written as = in many languages. The algorithm sorts the list v in place, meaning it will modify, or mutate, the list given to the Insertion-Sort function. One will notice that the operation swap is usually not a basic operation in most languages so here is the simple pseudocode for swap.

temp <- v[j]
v[j] <- v[j-1]
v[j-1] <- temp

With the above pseudocode, translating it to your favorite programming language is trivial. Here it is written in python.

def insertion_sort(v):
    for i in range(1, len(v)):
        j = i
        while j > 0 and v[j-1] > v[j]:
            v[j], v[j-1] = v[j-1], v[j]
            j = j - 1

The python code is almost a literal copy and paste of the pseudocode, which shows off the popular idea on how python is almost like pseudocode. The line v[j], v[j-1] = v[j-1], v[j] is how you perform a swap operation in python.

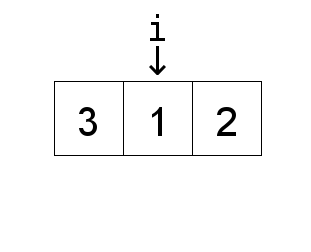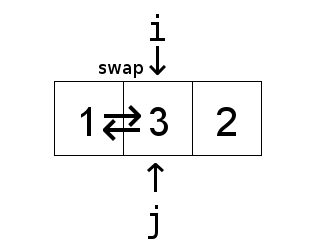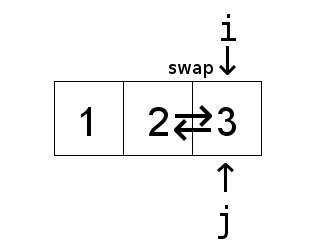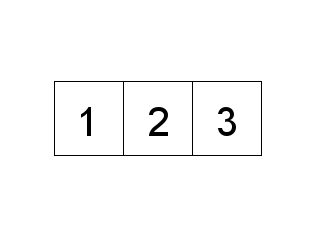
Now to explain the basic idea behind the above insertion sort algorithm. The algorithm treats the front of the list, that is elements with index less than i, as a list that is already sorted and elements that are greater than i as elements which need to be sorted. This is why the algorithm starts from 1 because sorting a list of length 1 is trivial, it is already sorted. So the first loop goes through the unsorted part of the list, "taking out" the element, and then inserting it into the the sorted part of the list. The insertion part of the algorithm is the inner while loop, which keeps swapping elements from the tail end of the sorted list until it reaches the correct spot.

The behavior of this algorithm is also pretty straight forward. In the best case, the list is already sorted and the algorithm takes linear time or O(n). The algorithm will go through the list and try to insert the element to only find v[j-1] > v[j] to be false and thus no need to swap the element. For the worst case insertion sort takes quadratic time or O(n²), the worst case being the list is in reverse sorted order. It is the worst case because at each element in the list, it must swap that element until it reaches the front of the list. For memory, the algorithm sorts the list in place and thus is constant space or O(1). The insertion sort algorithm I listed here can actually be improved to make it slightly faster, but I leave that as an exercise for the reader (Hint: it is mentioned on Wikipedia).

Insertion Sort on Linked Lists

The second variation is an algorithm that works on linked lists or sometimes known as cons cells in other programming languages. This algorithm is written as a recursive function.

Insertion-Sort(l)
    if l is the empty list
        return the empty list
    else
        return Insert(Insertion-Sort(rest of l), head of l)

The above pseudocode is an example of the algorithm. There is of course one problem with the above pseudocode, Insertion-Sort uses the operation of Insert to insert an element into an already sorted list. Insert isn't a basic operation so we must provide an Insert algorithm for lists.

Insert(l, n)
    if l is the empty list
        return a list with the element n
    else if n <= the head of l
        return a list with the element n as the new head of list l
    else
        return a list with Insert(rest of l, n))

Now we should be able to implement the Insertion Sort algorithm in a programming language. I decided to use the Scheme programming language because of lists being native to the language.

(define (insertion-sort l)
  (if (null? l)
      '()
      (insert (insertion-sort (cdr l)) (car l))))

(define (insert l n)
  (cond ((null? l) (list n))
        ((<= n (car l)) (cons n l))
        (else (cons (car l) 
                    (insert (cdr l) n)))))

For those unfamiliar with the Lisp family of languages, here is a break down of some of the operations performed above. null? is a procedure to check for the empty list, car is a procedure to get the first element of a list, cdr is the procedure to get the list without the first element, cons is the procedure to create pairs which form the linked lists of lisp. So (cons x y) with y being a list (a b) creates a list (x a b). cond is a special form similar to if except with multiple clauses in the form (question answer), where if question evaluates to true, then answer is evaluated and returned as the result.

(insertion-sort '(3 1 2))
(insert (insertion-sort '(1 2)) 3)
(insert (insert (insertion-sort '(2)) 1) 3)
(insert (insert (insert (insertion-sort '()) 2) 1) 3)
(insert (insert (insert '() 2) 1) 3)
(insert (insert '(2) 1) 3)
(insert '(1 2) 3)
(cons 1 (insert '(2) 3))
(cons 1 (cons 2 (insert '() 3)))
(cons 1 (cons 2 '(3)))
(cons 1 '(2 3))
'(1 2 3)

The idea behind this linked list version of insertion sort is to take each element from the list and then insert it into the sorted version of the list. So this recursive algorithm has to have a base case, which is if the list l is the empty list. Well, how do you sort the empty list? Of course, it is just the empty list. Now if the list isn't empty, we need to sort it, so the recursive step is to sort the rest of l. With the result of the recursive call, we have a sorted list without the first element of l, so we then insert the the first element l into the sorted list. The insert algorithm is complex enough to need an explanation as well. The insert algorithm is also recursive with the same base case of the list l being empty, so we just return a new list with the number n. The next base case is when n is less than or equal to the head of list l, so the proper action is to cons n to be the new head of l. The recursive step is when n isn't in the correct position, so we cons the current head of l onto the list with n inserted into it.

The behavior of the list insertion sort is similar to the first insertion sort. The best case is when the list is already sorted which will give you linear time or O(n). What the algorithm does is it tries to insert the head of l onto the already sorted list, the head will just be cons to the front of it. The worst case is also the same, the list is in reverse sorted list and thus has quadratic time or O(n²). Memory is a different story, this version of the algorithm creates a new list instead of sorting in place. The best case, when the list is already sorted, the algorithm copies the elements to the new list and is just linear space or O(n). The worst case is the list is in reverse sorted order, the insert algorithm creates a new list each time n is inserted into l which is quadratic space or O(n²). The above algorithm can also be improved, insertion sort can be made into an iterative process and the insert algorithm can also insert into the list by mutating it.